(Vocabulario de Seguros)
________________________________
EM 14. PROMEDIOS MÓVILES - Experium Markets
Media móvil
En estadística, una media móvil es un cálculo utilizado para analizar un conjunto de datos en modo de puntos para crear series de promedios. Así las medias móviles son una lista de números en la cual cada uno es el promedio de un subconjunto de los datos originales.
Por ejemplo, si se tiene un conjunto de 100 datos el primer valor de la serie de medias móviles podría ser el promedio de los primeros 25 términos, luego el promedio de los términos 2 al 26, el tercer elemento de los términos 3 al 27 y así, hasta por último el promedio de los últimos 25 números del 76 al 100.
Una serie de medias móviles puede ser calculada para cualquier serie temporal. Se usa para demanda estable, sin tendencia ni estacionalidad; suaviza las fluctuaciones de plazos cortos, resaltando así las tendencias o ciclos de plazos largos.
En estadística, una media móvil es un cálculo utilizado para analizar un conjunto de datos en modo de puntos para crear series de promedios. Así las medias móviles son una lista de números en la cual cada uno es el promedio de un subconjunto de los datos originales.
Por ejemplo, si se tiene un conjunto de 100 datos el primer valor de la serie de medias móviles podría ser el promedio de los primeros 25 términos, luego el promedio de los términos 2 al 26, el tercer elemento de los términos 3 al 27 y así, hasta por último el promedio de los últimos 25 números del 76 al 100.
Una serie de medias móviles puede ser calculada para cualquier serie temporal. Se usa para demanda estable, sin tendencia ni estacionalidad; suaviza las fluctuaciones de plazos cortos, resaltando así las tendencias o ciclos de plazos largos.
Índice
Media móvil simple[editar]
La media móvil previa[editar]
Una media móvil simple (Moving Average) es la media aritmética de los datos anteriores. En esta técnica elemental de predicción, cuanto más grande sea , mayor será la influencia de los datos antiguos. En contrapartida, si se selecciona una baja, se tendrán en cuenta datos más recientes para nuestra predicción.
De acuerdo a lo enunciado con anterioridad, concluimos que la elección de influenciará decisivamente nuestra predicción. Dependiendo del tipo de datos de serie temporal analizados podremos adaptar eficazmente nuestra predicción a los mismos. Así, si se elige un bajo, nuestra predicción tendrá una alta capacidad para responder rápidamente ante fluctuaciones o variaciones significativas en los datos de un período a otro. Sin embargo, la predicción en este caso estará altamente influenciada por efectos aleatorios. Por otro lado, la elección de un muy alto provocará que, aunque se filtre la existencia de efectos aleatorios, nuestras predicciones presenten una adaptación lenta ante fluctuaciones significativas en los datos de períodos más recientes, pues dicha predicción estará teniendo en cuenta el valor de datos antiguos.
La simplicidad de esta técnica hace que sea objeto de críticas en lo que refiere a su consideración equitativa de datos recientes y datos antiguos, sobre todo cuando el objeto de la predicción son variables cuya variabilidad en el corto plazo es importante para obtener una predicción eficaz, v.gr: análisis de demanda, nº ventas, etc. Además, en presencia de una tendencia en la serie de datos, la media movil simple causa problemas de predicción.
Una media móvil simple (Moving Average) es la media aritmética de los datos anteriores. En esta técnica elemental de predicción, cuanto más grande sea , mayor será la influencia de los datos antiguos. En contrapartida, si se selecciona una baja, se tendrán en cuenta datos más recientes para nuestra predicción.
De acuerdo a lo enunciado con anterioridad, concluimos que la elección de influenciará decisivamente nuestra predicción. Dependiendo del tipo de datos de serie temporal analizados podremos adaptar eficazmente nuestra predicción a los mismos. Así, si se elige un bajo, nuestra predicción tendrá una alta capacidad para responder rápidamente ante fluctuaciones o variaciones significativas en los datos de un período a otro. Sin embargo, la predicción en este caso estará altamente influenciada por efectos aleatorios. Por otro lado, la elección de un muy alto provocará que, aunque se filtre la existencia de efectos aleatorios, nuestras predicciones presenten una adaptación lenta ante fluctuaciones significativas en los datos de períodos más recientes, pues dicha predicción estará teniendo en cuenta el valor de datos antiguos.
La simplicidad de esta técnica hace que sea objeto de críticas en lo que refiere a su consideración equitativa de datos recientes y datos antiguos, sobre todo cuando el objeto de la predicción son variables cuya variabilidad en el corto plazo es importante para obtener una predicción eficaz, v.gr: análisis de demanda, nº ventas, etc. Además, en presencia de una tendencia en la serie de datos, la media movil simple causa problemas de predicción.
La media móvil central[editar]
En lugar de utilizar sólo datos anteriores, se utilizan también datos posteriores a aquél del cual se quiere obtener la media.
En lugar de utilizar sólo datos anteriores, se utilizan también datos posteriores a aquél del cual se quiere obtener la media.
Media móvil ponderada[editar]
La media móvil ponderada es una media multiplicada por ciertos factores, que le dan determinado peso a determinados datos. La media móvil ponderada (Weighted Moving Average) desarrolla y mejora las aplicaciones de la media móvil simple. Se trata de la media aritmética de los valores anteriores ponderados según diferentes criterios. De esta forma, se superan los inconvenientes que ofrece la técnica de media móvil simple pues, en función de las características de los datos analizados podremos decidir si darle mayor importancia a datos más antiguos o más recientes. Esta técnica será más eficiente que la media móvil simple a la hora de adaptar rápidamente el valor de la predicción a fluctuaciones en los datos recientes (v.gr: dándole una alta ponderación a los valores más nuevos).
La media móvil ponderada es una media multiplicada por ciertos factores, que le dan determinado peso a determinados datos. La media móvil ponderada (Weighted Moving Average) desarrolla y mejora las aplicaciones de la media móvil simple. Se trata de la media aritmética de los valores anteriores ponderados según diferentes criterios. De esta forma, se superan los inconvenientes que ofrece la técnica de media móvil simple pues, en función de las características de los datos analizados podremos decidir si darle mayor importancia a datos más antiguos o más recientes. Esta técnica será más eficiente que la media móvil simple a la hora de adaptar rápidamente el valor de la predicción a fluctuaciones en los datos recientes (v.gr: dándole una alta ponderación a los valores más nuevos).
Media móvil exponencial[editar]
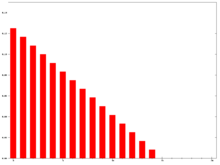
La media móvil exponencial es una media móvil ponderada exponencialmente. Se trata de la media aritmética de los valores anteriores con factores de ponderación que decrecen exponencialmente. La ponderación para cada punto de datos más antiguo decrece exponencialmente, nunca llegando a cero. El gráfico a la derecha muestra un ejemplo de la disminución de la ponderación. Da mayor importancia a los datos más recientes. Esta técnica será más eficiente que la media móvil simple y la media móvil ponderada a la hora de adaptar rápidamente el valor de la predicción a fluctuaciones en los datos recientes (v.gr: dándole una alta ponderación a los valores más nuevos).
La media móvil exponencial es una media móvil ponderada exponencialmente. Se trata de la media aritmética de los valores anteriores con factores de ponderación que decrecen exponencialmente. La ponderación para cada punto de datos más antiguo decrece exponencialmente, nunca llegando a cero. El gráfico a la derecha muestra un ejemplo de la disminución de la ponderación. Da mayor importancia a los datos más recientes. Esta técnica será más eficiente que la media móvil simple y la media móvil ponderada a la hora de adaptar rápidamente el valor de la predicción a fluctuaciones en los datos recientes (v.gr: dándole una alta ponderación a los valores más nuevos).
Promedio móvil simple
En aplicaciones financieras, un "promedio móvil simple" (PMS) es la media no ponderada de los datos "n" anteriores. Sin embargo, en ciencia e ingeniería, la media normalmente se toma de una cantidad igual de datos en cualquier lado de un valor central. Esto garantiza que las variaciones en la media estén alineadas con las variaciones en los datos en lugar de desplazarse en el tiempo.
Un ejemplo de una media de ejecución ponderada por igual para una muestra de precio de cierre de día n es la media de los precios de cierre de los días anteriores de n días. Si esos precios son la fórmula es:
Al calcular los valores sucesivos, un nuevo valor entra en la suma y un valor antiguo se elimina, lo que significa que una suma completa cada vez es innecesaria para este caso simple.
El período seleccionado depende del tipo de movimiento de interés, como corto, intermedio o largo plazo. En términos financieros, los niveles medios móviles pueden interpretarse como soporte en un mercado en baja, o resistencia en un mercado en alza, en un análisis técnico.
Si los datos utilizados no están centrados en torno a la media, un promedio móvil simple rezaga el último punto de referencia a la mitad del ancho de la muestra. Una PMS también puede verse desproporcionadamente influenciado por puntos de referencia anteriores o nuevos datos entrantes. Una característica del PMS es que si los datos tienen una fluctuación periódica, la aplicación de una PMS de ese período eliminará esa variación (el promedio siempre contiene un ciclo completo). Pero rara vez se encuentra un ciclo perfectamente regular.1
Para varias aplicaciones, es ventajoso evitar el cambio inducido al usar solo datos "pasados". Por lo tanto, se puede calcular una media móvil central , utilizando datos igualmente espaciados a cada lado del punto en la serie donde se calcula la media. La derivación y propiedades de la media móvil central simple se dan en completo en Filtro Savitzky-Golay. Esto requiere el uso de un número impar de puntos de referencia en la ventana de muestra.
Un inconveniente principal del PMS es que deja pasar una cantidad significativa de la señal más corta que la longitud de la ventana. Peor aún, en realidad lo invierte . Esto puede conducir a resultados inesperados, como picos en el resultado suavizado que aparecen donde había valles en los datos. También conduce a que el resultado sea menos uniforme de lo esperado ya que algunas de las frecuencias más altas no se eliminan correctamente.







No hay comentarios:
Publicar un comentario